Linguistics 105 * Words and Sounds

Lecture Number Six

Phonemes and Allophones

1. Phonemes
   1. The Minimal Pair
      1. A minimally phonologically distinctive pair of words establishes a minimal distinctive linguistic sound, known as a PHONEME, from among the acoustically distinguishable sounds in a language, known as the phones of the language.

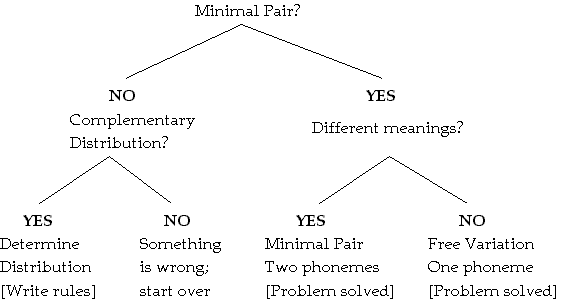
         a PHONEME is the minimal distinctive linguistic sound

      2. A minimal distinctive sound is one which can distinguish one word from another when all other sounds are identical. These p hones are said to be in CONTRASTIVE DISTRIBUTION. To establish the phonemes of a language such MINIMAL PAIRS, two words differing in just one distinguishable sound (hence 'minimal'), must be found for all the phonemes.

      Table 1: Minimal Pairs
      Minimal Pair	Context	Phonemes
      [bêd] : [bød]	[b___d]	/ê/ : /ø/
      [bøt] : [bød]	[bø___]	/d/ : /t/
      [bøt] : [pøt]	[___øt]	/b/ : /p/

       

      If you cannot find a minimal pair, the phones are said to be in non-contrastive distribution. They may be in COMPLEMENTARY DISTRIBUTION or in FREE VARIATION.

   
   

2. Complementary Distribution
   1. Complementary Distribution indicates that two basic sounds are not independent PHONEMES, but conditioned variants of the same phoneme, of the same minimally distinctive sound. Non-contrastive variants of a phoneme are called ALLOPHONES.

      an ALLOPHONE is one of the non-contrastive variations of a minimal distinctive linguistic sound

   2. Sounds are in complementary distribution when one occurs under condition A but never B, while the other occurs under condition B but never A. That is, the allophonic variation is predictable from the environment. For example, aspirated phones are allophones of nonaspirated phones in English but comprise phonemes in Khmer:

      Table 2: Aspiration in English & Khmer
      Potential Pairs		Context	Phonemes?
      English Aspiration
      [spøt]	[pßøt]	*[spß]	Phoneme: /p/
      [stek]	[tßeyk]	*[stß]	Phoneme: /t/
      [skeyt]	[kßet]	*[skß]	Phoneme: /k/
      Khmer Aspiration
      [paa] "father"	[pßaa] "silk cloth"	[minimal pair ]	Phonemes: /p/, /pß/
      [tuu] "chest"	[tßuu] "relaxed"	[minimal pair ]	Phonemes: /t/, /tß/
      [kae] "to repair"	[kßae] "month"	[minimal pair ]	Phonemes: /k/, /kß/

   
   

3. Free Variation
   1. Two sounds do not represent two separate phonemes if they are in FREE VARIATION; that is, if you may use one in any position you may use the other without any semantic effect. For example, aspiration may be omitted from stops at the end of words in English, too; however, whether it is dropped or not is indifferent; the meaning of the word does not change.

   Table 3: Free Variation
   Free Variants	Distribution	Phoneme
   [stip] : [stipß]	___#	Phoneme: /p/
   [spøt] : [spøtß]	___#	Phoneme: /t/
   [støk] : [støkß]	___#	Phoneme: /k/

   
   Summary
   

   1. Each phone represents a separate phoneme, /x/, /y/
      1. if you can find a contrastive pair and
      2. the sounds [x] and [y] are not in free variation, that is, there is a difference in meaning

   2. If there are no minimal pairs and distribution is complementary,
      1. the two (allo)phones [x], [y] are variants of the same phoneme /x/ and
      2. you must provide a phonological rule to explain the relation between the two variants.
   3. If there are no minimal pairs and distribution is free,
      1. the two (allo)phones [x], [y] are variants of the same phoneme /x/ and
      2. the variation is due to dialectical variation or personal linguistic habits.

   Algorithm for Problem-Solving in Phonology

   

   
   

4. A Catalog of Basic Linguistic Symbols

   [Use these symbols in the solutions to the homework and test problems]

© 1996-2000 yourDictionary.com, Inc.