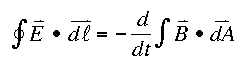Faraday's Law
This equation is called Faraday's law, one of Maxwell's equations. Faraday's law describes the fact that a changing magnetic flux through an arbitrary area induces an electric field that circulates around the perimeter of that area.
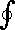
The Line Integral
The integral sign with a little circle means that we are integrating, or summing, around a closed curve. The shape of the curve is arbitrary, but it must coincide with the perimeter of the area used in computing the magnetic flux. In Faraday's law we are summing the induced electric field, so we must imagine, for each little element of length, dl, taking the dot product of the electric field vector at the element with the element of length itself.In the movie, the electric field is shown at several points around each of several circles. If you look carefully, you'll notice that the field is larger on the larger circles than on the smaller circles. This is because the larger circles enclose more magnetic flux.
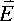
The induced electric field
The induced electric field "circulates" around the changing magnetic flux. In particular, there is no induced electric field at any instant of time unless the flux is changing at that instant of time. In fact, there can even be an induced electric field when the magnetic flux is zero, provided that the flux is changing. The red bar in the movie indicates the strength and direction of the induced electric field (upward bar for clockwise field).Try to understand the direction of the induced electric field from the right-hand-rule relation connecting the direction you integrate around the closed loop and the direction of the positve normal to the loop.

The dot
Remember that the dot in a dot product means you multiply together not only the magnitudes of the two vectors but also the cosine of the angle between them.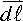
The length element
The integral sign with a little circle means that we are integrating, or summing, around a closed curve. The shape of the curve is arbitrary, but it must coincide with the perimeter of the area used in computing the magnetic flux. In Faraday's law we are summing the induced electric field, so we must imagine, for each little element of length, dl, taking the dot product of the electric field vector at the element with the element of length itself.In the movie, the electric field is shown at several points around each of several circles. If you look carefully, you'll notice that the field is larger on the larger circles than on the smaller circles. This is because the larger circles enclose more magnetic flux.
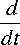
The time derivative
The flux through a loop can change with time in several different ways: the magnetic field can change, the shape of the loop can change, and the orientation of the loop with respect to the magnetic field can change. If, at any instant of time, none of these things are changing, then there is no induced electric field at that instant.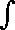
The surface integral
The integral sign without a little circle indicates we are summing over an open surface (like one side of a piece of paper). In Faraday's law we integrate the magnetic flux, B (a vector), over the area of some open surface. The resulting integral is called the magnetic flux through the surface.To visualize the surface integral you must imagine, at each little element of area, dA, you take the dot product of the magnetic field vector at that point in space with the area element. In doing the dot product you must know which way the positive normal to the element points. The direction you choose for the positive normal determines the direction you must integrate around the perimeter of the area in computing the line integral of the induced electric field by the right-hand-rule.
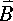
The magnetic field
The magnetic field in Faraday's law is produced by some magnet or current-carrying wire, which does not appear directly in Faraday's law. The strength and direction of the magnetic field is shown by the blue arrow and also by the blue bar. But the existence of a magnetic field does not mean there is necessarily an induced electric field. In order to create an electric field the magnetic flux through an area must be changing with time. In the movie, the magnetic field reaches a maximum in either the upward or downward direction, and remains constant for a short time. During this brief interval the induced electric field, as shown by the red bar, is zero.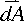
The area element
The integral sign without a little circle indicates we are summing over an open surface (like one side of a piece of paper). In Faraday's law we integrate the magnetic flux, B (a vector), over the area of some open surface. The resulting integral is called the magnetic flux through the surface.To visualize the surface integral you must imagine, at each little element of area, dA, you take the dot product of the magnetic field vector at that point in space with the area element. In doing the dot product you must know which way the positive normal to the element points. The direction you choose for the positive normal determines the direction you must integrate around the perimeter of the area in computing the line integral of the induced electric field by the right-hand-rule.
 Back to main equation page
Back to main equation page